Wharton health care management professor Ashley Swanson has new research that looks at the gender gap among top math students in high school. Closing the gender gap in school performance is an important step toward shrinking the gender gap in pay when these students enter the workforce, so the research has far-reaching implications. Swanson spoke to Knowledge at Wharton about her paper, “Dynamics of the Gender Gap in High Math Achievement,” which was co-authored with MIT economics professor Glenn Ellison.
An edited transcript of the conversation follows.
Knowledge at Wharton: What was the inspiration for this research?
Ashley Swanson: My co-author, Glenn Ellison, and I have been working on this topic for a long time. He has been a longtime coach of his daughter’s math teams and also has authored a series of math books for children. I participated on the math team myself as a teenager, although the American Mathematics Competition (AMC) that we studied wasn’t offered at my school.
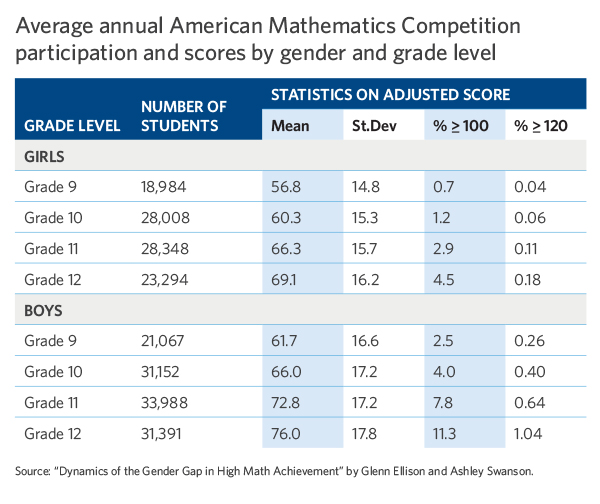
Our first paper documents this really large gender gap at high levels of performance, much bigger than we see for average performance. The gender gap at average levels of math performance has declined a lot over time, which is great. But if you look at these higher levels — like the 95th percentile or the 99th percentile — the gender gap is high and growing as you go to higher and higher levels of performance, which is not so good.
We see a much higher gender gap at these higher levels of performance than we see even at the, say, SAT 800 level. At the highest levels of performance, we observe in our data the gender gap is about 10-to-1. This is something we’ve observed looking at just 2007. This is just a snapshot of data. We speculated that this is something we can track over time, so that’s what we were trying to get at in this paper. Is this something that evolves over time? If so, how does it evolve over time?
Knowledge at Wharton: Can you explain how this competition works and what you observed when you looked at the results over time?
Swanson: This competition is offered over the course of high school. Students often take it from ninth through 12th grade. It’s offered in a selected set of schools, so it’s only offered in about 3,000 U.S. high schools. Even within that special subset of students, we observed some really striking dynamics.
We’re tracking students from 1999 to 2007 … a series of cohorts from ninth through 12th grade. We observe that these students’ participation and performance changes a little bit over time. The strongest feature that pops out of our data is that there’s a large gender gap already by the ninth grade, and it widens over the course of the high school years.
For example, we find a 4.6-to-1 male/female ratio among the 500 highest-scoring ninth-graders on the AMC. So, there’s already a really dramatic difference between boys’ performance and girls’ performance by ninth grade, and it grows a lot over time. This widens to about a 7.4-to-1 ratio of boys to girls among the 500 highest-scoring 12th-graders.
Knowledge at Wharton: What are some possible explanations for why this is happening?
Swanson: One way of answering this question is to investigate what happens mechanically. Is it that high-performing girls are more likely to drop out of the contest? Is it that talented girls are less likely to drop into the contest over time after the ninth grade? Is it that talented girls are less likely to improve enough from year to year to stay highly ranked within the program? The short answer is yes. Each of those factors cuts against girls and contributes to a widening of the gender gap over time. We find that the most important of these factors is that fewer girls are making large enough increases from year to year to move into the top-ranked groups, but each of those factors plays a part.
Knowledge at Wharton: A couple of the factors that you mention in the paper are that female students might react differently to disappointment than male students, that they might be less interested in this type of competition, or that they might have some competing priorities. Do you feel this speaks to innate gender differences, or could this be something they’re also learning as they come up in school?
“We know that girls and boys are treated differently, even at early ages … in terms of the expectations that are directed at them.”
Swanson: It’s hard for us to say definitively what is driving these differences, but we can speak to whether these differences are a good thing or a bad thing in some respects.
For example, as you allude to, we document this really striking finding about how students react to disappointment. We focus on this cut-off at which students progress to the next level of these math competitions. If you score highly enough on the American Mathematics Competition exams, you move on to an invitational exam. This is really exciting for students. It’s something that extends their math competition career for the year, and it’s something that people would be excited to put on their college applications.
But what we observe is that students that just miss the cut-off to progress to the invitational exam are more likely to drop out. Now, this is not a rational response. They’ve just gotten a signal that they’re really close to being good. With a little bit more effort, they can move onto the next level of competition next year and put this exciting thing on their college applications. But instead, they’re disappointed and drop out. This is about a 10% effect for boys. It’s more like a 15% effect for girls, so girls are much more reactive to this disappointment. This is a problem for all students, but it’s a stronger problem for girls. Does that mean that girls are more disappointed than boys are? It’s not clear. Perhaps they’re just as disappointed, but girls have other things going on that are going to divert their attention and their energy when they drop out of these contests. Maybe they’re going to participate in other after-school activities or something like that. We can’t quite say.
You also asked whether this is something about innate differences in the genders. That’s a really complicated question because these things build over time. We know that girls and boys are treated differently, even at early ages, by their parents, by their teachers, in terms of the expectations that are directed at them. So, we can’t rule anything out about innate differences in the genders just looking at this competition data. However, we think it would be a good idea to start with some of these factors regarding differential treatment before assuming that it’s innate differences in the genders.
Knowledge at Wharton: But you also mention a study in the paper about the differences between how females versus males react to this type of competition, which has a game-show style structure.
Swanson: Yes, there’s a lot of really cool research indicating that girls and boys have different preferences over competition, and that might contribute to how they react to disappointment in competitive settings. However, there’s a chicken-and-egg problem here. Are girls and boys born reacting differently to competition, or is this something that evolves over time, given how they’re treated and socialized? I think that’s an open question, and we need more research on this topic.
Knowledge at Wharton: You said the gap between more average performers in math is narrowing, but do you see some trickle-downs with this research for the greater population of students — the B students, the C students, or even the D or F students?
“High performance in math is important in its own right.”
Swanson: I don’t think so. Our findings probably don’t generalize outside this topic. Girls perform just as well or better than boys on the SAT verbal and writing components, and the gender gap on average levels of performance is kind of negligible at this point in time. However, high performance in math is important in its own right. High-achieving students make important contributions to science and technology, and advanced math courses taken in high school are associated with higher earnings 10 years later.
Knowledge at Wharton: What can educators do to help close this performance gap?
Swanson: Something we found in our previous research is that the really high-performing girls and really high-performing boys are coming from very different schools. The highest-performing boys are coming from very good schools — call it a 93rd percentile school. The highest-performing girls are coming from the best-of-the-best schools. We’d like to understand what these best-of-the best schools are doing differently to bring the girls up to these high levels of performance that other schools are not doing. Perhaps they’re creating a different social environment. Perhaps they’re treating girls and boys more equally in these schools. We’d like to see more research on this topic.
One thing that’s a little bit discouraging about some of our previous research is that the best-of-the-best schools are special in ways that might be hard to replicate. We know that they offer more advanced math classes, and that’s something that other schools can do a better job at. However, they also tend to have these long-serving, devoted, star teachers, and I’m pretty sure cloning technology is not that far along.
Knowledge at Wharton: These tests are coming for students at a pivotal point. They’re about to go to college. These high achievers are trying to figure out where they want to go with their careers, and women have been traditionally underrepresented in STEM (science, technology, engineering and math) careers. Do you feel like there’s concern that the results you’re seeing on these tests might also reflect what types of careers that female students are choosing?
Swanson: This is something we’re really interested in because, as I said before, advanced math courses taken in high school affect earnings 10 years later. Gender differences in college majors are an important determinant of the pay gap between college-educated men and women, and we know that these dynamic effects don’t stop at high school or at college. There are large, documented differences in the progression of men’s and women’s careers as a function of some of these factors we talked about before — like drop-ins, drop-outs, and how people advance — conditional on staying in math competitions or in the job market. This is really important for some of the things that we’re worried about later in life, like glass ceilings and pay gaps. More research is definitely needed on this topic.